Answer:

Explanation:
Cubic polynomial in intercept form:
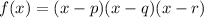
where p, q and r are the zeros.
Given:
- Zeros at x = -4 and x = 6
- Passes through the point (2, 36)
Substitute the zeros into the formula:

Substitute the point into the equation and solve for p:
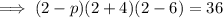
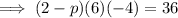
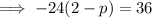

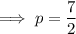
Therefore:
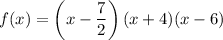
Factor out ¹/₂ from the first parentheses:
