Answer:
Explanation:
Question 1.

Move all terms containing
 to the left side of the inequality.
to the left side of the inequality.
Subtract
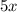 from both sides of the inequality.
from both sides of the inequality.
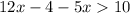
Subtract
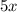 from
from
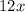 .
.
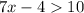
Move all terms not containing
 to the right side of the inequality.
to the right side of the inequality.
Add 4 to both sides of the inequality.
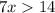
Divide each term in
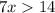 by 7 and simplify.
by 7 and simplify.
The answer can be written as
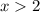 or (2,∞)
or (2,∞)
Question 2.

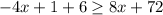
Move all terms containing
 to the left side of the inequality.
to the left side of the inequality.
Subtract
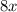 from both sides of the inequality.
from both sides of the inequality.
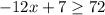
Move all terms not containing
 to the right side of the inequality.
to the right side of the inequality.
Subtract 7 from both sides of the inequality.
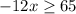
Divide each term in
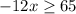 by − 12 .
by − 12 .
When multiplying or dividing both sides of an inequality by a negative value, flip the direction of the inequality sign.
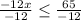
The answer can be written as
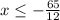 or (−∞,−
or (−∞,−
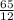 ]
]