Question

If
`2^{16^(x) }=16^{2^(x) }` how come
`16^(x)=4(2^x)`

Answer 1

the log of the first equation gives the second

Explanation:

You want to know why ...

`\displaystyle 2^(16^x)=16^(2^x)`

means ...

`16^x=4\cdot2^x`

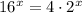
Logarithms

Taking logs to the base 2 of the original equation, we get ...

`16^x=(2^x)\log_2{16}\\\\\boxed{16^x=4\cdot2^x}`

__

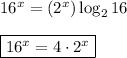
Additional comment

This is the relation you asked about. It can be solved by taking logs one more time (base 2).

4x = 2 +x

3x = 2 . . . . . . . subtract x

x = 2/3 . . . . . . . divide by 3

This is the only value of x for which all of these exponential expressions have the relations given.

The relevant log relation is ...

log(a^b) = b·log(a)