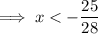Answer:
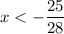
Explanation:
Given inequality:
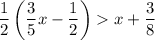
Distribute:
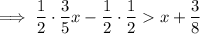
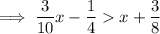
Add 1/4 to both sides:

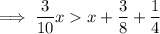
Subtract x from both sides:
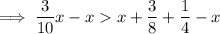
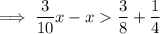
Rewrite fractions so that the denominators are the same on each side fo the inequality:
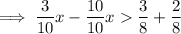
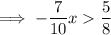
Multiply both sides by 10/7:
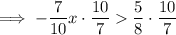
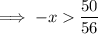

Divide both sides by -1 (remembering to reverse the inequality sign):