Question

Each of the two drums and connected hubs of 250 mm radius has a mass of 105 kg and a radius of

gyration about its center of 370 mm. Calculate the angular acceleration of each drum. Friction in each
bearing is negligible.

Answer 1

the angular acceleration of each drum depends on the applied force F. If the force is known, then the angular acceleration can be calculated. If the force is not known, then the angular acceleration cannot be calculated.

Step-by-step explanation:

To find the angular acceleration of each drum, we can use the equation for rotational dynamics:

`I * alpha = F * r`

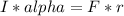
where I is the moment of inertia of the drum, alpha is the angular acceleration, F is the applied force, and r is the distance from the center of rotation to the point where the force is applied.

In this case, the moment of inertia of each drum is given by:

`I = mr^2`

where m is the mass of the drum and r is the radius of gyration. Substituting this expression into the equation above, we get:

`(m * r^2) * alpha = F * r`

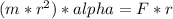
Solving for alpha, we find that:

`alpha = F * r / (m * r^2)`

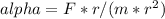
Substituting the given values, we find that the angular acceleration of each drum is:

`alpha = F * 250 mm / (105 kg * (370 mm)^2)`

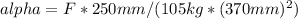
This equation can be simplified to:

`alpha = F / (7.29 * 105 kg)`

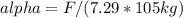
So the angular acceleration of each drum depends on the applied force F. If the force is known, then the angular acceleration can be calculated. If the force is not known, then the angular acceleration cannot be calculated.