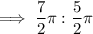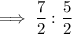Question

A rainbow-shaped logo is formed from three semicircles

Answer 1

7 : 5

Explanation:

`\boxed{\begin{minipage}{4 cm}\underline{Area of a semicircle}\\\\$A=(1)/(2) \pi r^2$\\\\where:\\ \phantom{ww} $\bullet$ $r$ is the radius.\\ \end{minipage}}`

If the diameter of the outer semicircle is 8 cm, then its radius is 4 cm.

Area of a semicircle with radius 4 cm:

`\implies A=(1)/(2) \pi \cdot 4^2`

`\implies A=(1)/(2) \pi \cdot 16`

`\implies A=8 \pi \; \sf cm^2`

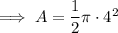
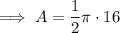
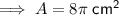
Area of a semicircle with radius 3 cm:

`\implies A=(1)/(2) \pi \cdot 3^2`

`\implies A=(1)/(2) \pi \cdot 9`

`\implies A=(9)/(2) \pi \; \sf cm^2`

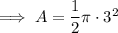
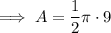
Area of a semicircle with radius 2 cm:

`\implies A=(1)/(2) \pi \cdot 2^2`

`\implies A=(1)/(2) \pi \cdot 4`

`\implies A=2\pi \; \sf cm^2`

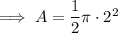
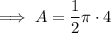
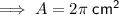
Area A

To find the area of section A, subtract the area of a semicircle with radius 3 cm from the area of a semicircle with radius 4 cm:

`\implies \textsf{Area A}=8 \pi - (9)/(2) \pi`

`\implies \textsf{Area A}= (7)/(2) \pi \; \sf cm^2`

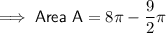
Area B

To find the area of section B, subtract the area of a semicircle with radius 2 cm from the area of a semicircle with radius 3 cm:

`\implies \textsf{Area A}=(9)/(2) \pi-2 \pi`

`\implies \textsf{Area A}=(5)/(2) \pi\; \sf cm^2`

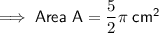
Therefore, the ratio of area A to area B is:

`\implies (7)/(2) \pi : (5)/(2) \pi`

`\implies (7)/(2) : (5)/(2)`

`\implies 7:5`