Question

For the function f(x) = x² - 8, find the slope of the secant line between x = -3
and x = 6.

Answer 1

Slope = 3

Explanation:

A secant is a straight line cutting a curve at two or more points.

Given function:

`f(x)=x^2-8`

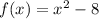
Find the values of y for the given x-values:

`\begin{aligned}\implies f(-3)&=(-3)^2-8\\&=9-8\\&=1\end{aligned}`

`\begin{aligned}\implies f(6)&=(6)^2-8\\&=36-8\\&=28\end{aligned}`

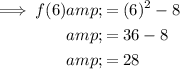
Therefore, the endpoints of the secant line are:

• (-3, 1)
• (6, 28)

`\boxed{\begin{minipage}{8cm}\underline{Slope Formula}\\\\Slope $(m)=(y_2-y_1)/(x_2-x_1)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.\\\end{minipage}}`

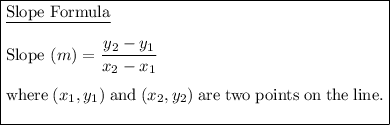
To find the slope of the secant line, substitute the found endpoints into the slope formula:

`\implies \textsf{Slope}=(28-1)/(6-(-3))=(27)/(9)=3`