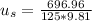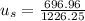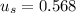Answer:
The coefficient of static friction be between the tires and the road is 0.568.
Step-by-step explanation:
Equation for Centripetal Force
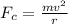
We know that the maximum static friction (at which the tires roll but do not slip) is
 , where
, where
 is the static coefficient of friction and
is the static coefficient of friction and
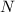 is the normal force. The normal force equals the car’s weight on level ground, so
is the normal force. The normal force equals the car’s weight on level ground, so
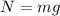 . Thus the centripetal force in this situation is
. Thus the centripetal force in this situation is
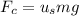
Now we have a relationship between centripetal force and the coefficient of friction. Therefore we can say
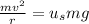
Lets solve for

Divide both sides by
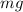 .
.
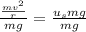
Simplify the right side by cancelling the common factor of
 .
.
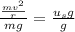
Simplify the right side by cancelling the common factor of
 .
.
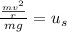
Simplify the left side by multiplying the numerator by the reciprocal of the denominator.
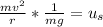
Combine the fractions.
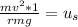
Simplify the left side by cancelling the common factor of
 .
.
Finally we get
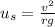
We are given
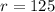
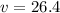
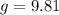
Substitute these values into our equation.