Question

Solving by Elimination: Solve the following system of equations using elimination:

3x + y = 16

-3x - 5y = -44

Answer 1

`\large\displaystyle\text{$\begin{gathered}\sf \bf{3x+y=16 } \end{gathered}$}\\ \large\displaystyle\text{$\begin{gathered}\sf \bf{-3x-5y=-44 } \end{gathered}$}`

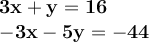
Adding the two equations we arrive at the elimination of x:

`\large\displaystyle\text{$\begin{gathered}\sf \bf{3x+y+(-3x-5y)=16-44 } \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\Rightarrow \ -4y=-28} \end{gathered}$}`

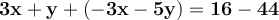
From the above equation we find directly that dividing both sides of the equation by −4 we get.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{y=(-28)/(-4)=7 } \end{gathered}$}`

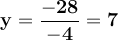
Now, we plug y=7 back into the other equation.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{3x+(7)=16 } \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\Rightarrow3x+(7)=16 } \end{gathered}$}`

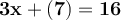
Simplifying constants:

`\large\displaystyle\text{$\begin{gathered}\sf \bf{3x+7=16 } \end{gathered}$}`

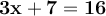
Putting x on the left hand side and the constants on the right hand side we get.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{3x=16-7 } \end{gathered}$}\\ \large\displaystyle\text{$\begin{gathered}\sf \bf{\ \ \Rightarrow3x=9} \end{gathered}$}`

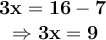
Then, solving for x, by dividing both sides of the equation by 3, the following is obtained.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{x=3} \end{gathered}$}`

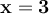
We will verify if the found solutions really satisfy the equations.

We plug 3x=3 and y=7 into the given equations and get.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{3\cdot(3)+(7)=16 } \end{gathered}$}\\ \large\displaystyle\text{$\begin{gathered}\sf \bf{-3\cdot(3)-5\cdot(7)=-44 } \end{gathered}$}`

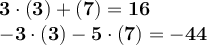
This confirms that the solutions found are real solutions of the system of equations.

Conclution

Therefore, based on the analysis performed with the elimination method, there is a unique solution, which is x=3,y=7.