Question

a 1 020-kg satellite orbits the earth at a constant altitude of 93-km. (a) how much energy must be added to the system to move the satellite into a circular orbit with altitude 210 km? how is the total energy of an object in circular orbit related to the potential energy? mj (b) what is the change in the system's kinetic energy? mj (c) what is the change in the system's potential energy?

Answer 1

Approximately
`5.4 * 10^(8)\; {\rm J}` of energy will be required. Total mechanical energy of this satellite is equal to
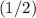`(1/2)` of its gravitational potential energy.

The kinetic energy of the system will decrease by approximately
`5.4 * 10^(8)\; {\rm J}` (a change of
`(-5.4) * 10^(8)\; {\rm J}`.)

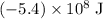The gravitational potential energy of the system will increase by approximately
`1.1* 10^(9)\; {\rm J}`.

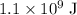Step-by-step explanation:

Let
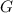`G` denote the gravitational constant. Let
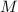`M` denote the mass of the Earth. Let
`r` denote the radius of the orbit. Let
`v` denote the orbital speed of the satellite. Let
`m` denote the mass of the satellite.

Assume that the gravitational attraction from the Earth
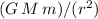`(G\, M\, m) / (r^(2))` is the only force on the satellite. The acceleration of the satellite will be:

`\begin{aligned}(\text{acceleration}) &= \frac{(\text{net force})}{(\text{mass})} \\ &= ((G\, M\, m) / (r^(2)))/(m)= (G\, M)/(r^(2))\end{aligned}`.

Since the satellite is in a uniform circular motion of orbital speed
`v` and radius
`r`, acceleration will be
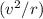`(v^(2) / r)` (centripetal acceleration.)

`\begin{aligned}(\text{acceleration}) &= (v^(2))/(r)\end{aligned}`.

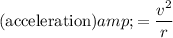Therefore:

`\begin{aligned}(v^(2))/(r) &= (\text{acceleration}) = (G\, M)/(r^(2))\end{aligned}`.

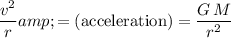Rearrange and solve for orbital speed
`v`:

`\begin{aligned}v^(2) &= (G\, M)/(r)\end{aligned}`.

`\begin{aligned}v &= \sqrt{(G\, M)/(r)}\end{aligned}`.

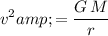With a mass of
`m`, the kinetic energy
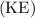`(\text{KE})` of this satellite will be:

`\begin{aligned}(\text{KE}) &= (1)/(2)\, m\, v^(2) \\ &= (1)/(2)\, m\, \left((G\, M)/(r)\right) = (G\, M\, m)/(2\, r)\end{aligned}`.

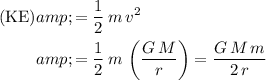The gravitational potential energy
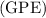`(\text{GPE})` of the satellite would be:

`\begin{aligned}(\text{GPE}) &= \left(-(G\, M\, m)/(r)\right)\end{aligned}`.

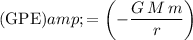The total mechanical energy of this satellite is the sum of
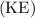`(\text{KE})` and
`(\text{GPE})`.

`\begin{aligned}(\text{KE}) + (\text{GPE}) &= \left((G\, M\, m)/(2\, r)\right) + \left(-(G\, M\, m)/(r)\right) = (-G\, M\, m)/(2\, r)\end{aligned}`.

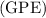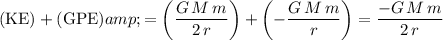Hence, the total (mechanical) energy of this satellite is
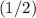`(1/2)` the value of potential energy.

The radius of the Earth is approximately
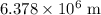`6.378 * 10^(6)\; {\rm m}`. At the initial orbit (
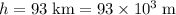`h = 93\; {\rm km} = 93* 10^(3)\; {\rm m}`,) the orbital radius will be approximately
`6.378 * 10^(6)\; {\rm m} + 9.3 * 10^(4)\; {\rm m} \approx 6.471 * 10^(6)\; {\rm m}`.

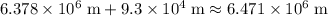• Kinetic energy:
  
  `\begin{aligned} & (\text{KE}) \\ =\; & (G\, M\, m)/(2\, r) \\ =\;& (6.6743 * 10^(-11)\; {\rm m^(3)\cdot kg^(-1) \cdot s^(-2)})\\ & (5.792* 10^(24)\; {\rm kg}) \\ & (1020\; {\rm kg}) \\ & (1/2) \\ & (1/(6.471 * 10^(6)\; {\rm m})) \\ \approx\; & 3.0467* 10^(12)\; {\rm J}\end{aligned}`.
  
• Gravitational potential energy:
  
  `\begin{aligned} & (\text{GPE}) = (-G\, M\, m)/(r) \approx (-6.0934) * 10^(10)\; {\rm J}\end{aligned}`.
  
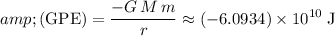• Total mechanical energy:
  
  `\begin{aligned} (\text{KE}) + (\text{GPE}) =\; & (-G\, M\, m)/(2\, r) \approx (-3.0467) * 10^(10)\; {\rm J}\end{aligned}`.

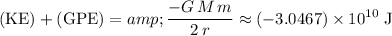At the new orbit (
`r = 210\; {\rm km} = 210 * 10^(3)\; {\rm m}`):

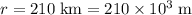• Kinetic energy:
  
  `\begin{aligned} (\text{KE}) = (G\, M\, m)/(2\, r) \approx 2.9926 * 10^(10)\; {\rm J}\end{aligned}`.
  
• Gravitational potential energy:
  
  `\begin{aligned} (\text{GPE}) =& (-G\, M\, m)/(r) \approx(-5.9852* 10^(10))\; {\rm J}\end{aligned}`.
  
• Total mechanical energy:
  
  `\begin{aligned} (\text{KE}) + (\text{GPE}) = -(G\, M\, m)/(2\, r) \approx\; &(-2.9926) * 10^(10)\; {\rm J}\end{aligned}`.

The energy that need to be added to the system is equal to the difference in total mechanical energy (
`(\text{GPE}) + (\text{KE})`):

`((-2.9926) * 10^(10)\; {\rm J}) - ((-3.0467) * 10^(10)\; {\rm J}) \approx 5.4 * 10^(8)\; {\rm J}`.

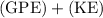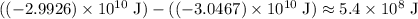Change in the kinetic energy of the system:

`(2.9926 * 10^(10)\; {\rm J}) - (3.0467* 10^(10)\; {\rm J}) \approx (-5.4) * 10^(8)\; {\rm J}`.

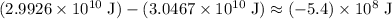In other words, the kinetic energy of the system would be reduced by approximately
`(-5.4) * 10^(8)\; {\rm J}`.

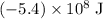Change in the gravitational potential energy of the system:

`\begin{aligned}& (-5.9852* 10^(10)\; {\rm J}) - (-6.0934* 10^(10)\; {\rm J})\approx 1.1 * 10^(9)\; {\rm J}\end{aligned}`.

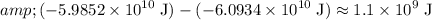In other words, the gravitational potential energy of the system would increase by approximately
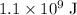`1.1 * 10^(9)\; {\rm J}`.