Question

Horizontal Transformations

Up to you if you want to do 14 I just want help on 13

Answer 1

Problem 13, part (a)

The notation w(x+7) means we replace the original input x with the new input x+7. This will move the xy axis 7 units to the right. If we kept the function curve held still, then the axis moving 7 units to the right gives the illusion the curve moves 7 units to the left.

In short: The w(x+7) means "move the curve 7 units to the left".

This movement will affect the domain and roots, but won't affect the range.

Originally the domain is
`-5 \le \text{x} \le 4`

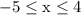
Subtract 7 from each endpoint to get the new domain to be
`-12 \le \text{x} \le -3`, which is the result of shifting the xmin and xmax 7 units to the left.

The roots (-3,0) and (2,0) will move to (-10,0) and (-5,0) respectively after shifting 7 units to the left.

The range doesn't get affected because we aren't shifting the graph up or down. Recall the range is the set of possible y values.

--------------

Answer:

• Domain:
  `-12 \le \text{x} \le -3`
• Range:
  `-2 \le \text{y} \le 10`
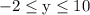
• Roots: (-10,0) and (-5,0)

============================================================

Problem 13, part (b)

We follow the same idea as the previous problem.

This time we shift the curve 9 units to the right. You can think of it like the xy axis moves 9 units to the left, but that gives the illusion the curve moves 9 units to the right.

--------------

Answer:

• Domain:
  `4 \le \text{x} \le 13`
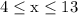
• Range:
  `-2 \le \text{y} \le 10`
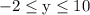
• Roots: (6,0) and (11,0)

============================================================

Problem 14

The parent function
`\text{y} = \sqrt{\text{x}}` has its left-most endpoint at (0,0).

This current graph has its left-most endpoint at (4,2)

Therefore, we shift the parent curve 4 units to the right and 2 units up.

Applying the "4 units right" transformation means we replace x with x-4.

Shifting "2 units up" means we stick a +2 at the end.

`\text{y} = \sqrt{\text{x}} \ \ \text{ ... parent function}\\\\\text{y} = \sqrt{\text{x}-4} \ \ \text{ ... shift 4 units right}\\\\\text{y} = \sqrt{\text{x}-4}+2 \ \ \text{ ... shift 2 units up}\\\\`

Therefore, Dewey has the correct equation.