Question

Solve with explanation

Answer 1

`\begin{cases} y=36-9x\\\\ 3x+(y)/(3)=12 \end{cases}\hspace{4.5em}\stackrel{\textit{substituting on the 2nd equation}}{3x+\cfrac{\stackrel{y}{36-9x}}{3}=12}\implies 3x+\cfrac{36}{3}-\cfrac{9x}{3}=12 \\\\\\ 3x+12-3x=12\implies 12=12 ~~ \textit{\LARGE what the?}`

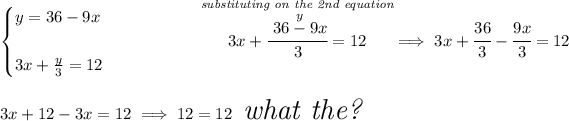
well, 12 is indeed equals to 12, however that's a bit cyclical, but is another way to say that the equations are really twins and thus there is infinitely many solutions, often you may encounter stuff like 0=0 or 13 = 13 or such, same thing, now, hmmmm let's simplify the 2nd equation a bit

`\begin{cases} \boxed{y=36-9x}\\\\ 3x+(y)/(3)=12 \end{cases} \\\\\\ \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{3}}{3\left( 3x+\cfrac{y}{3} \right)=3(12)}\implies 9x+y=36\implies \boxed{y=36-9x}`

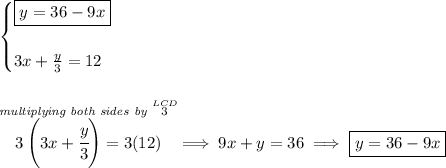
ahaaa!!, notice, the 2nd equation is really the 1st in disguise, so both equations are really twins, a solution occurs when the graph of both equations intersect, well, when we have twin equations they intersect everywhere, since the graph of the 2nd one is just pancaked on top of the 1st one, and since both go to infinity, we have just as many solutions, infinitely many solutions.