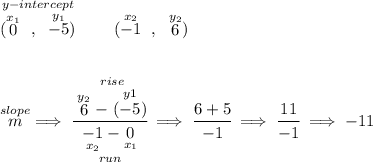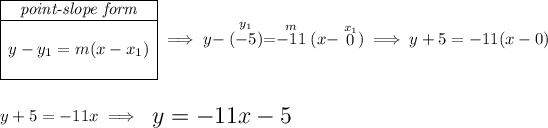Question

What is the equation of the line that passes through the point (-1,6) and has a y-intercept of -5

Answer 1

well, since the y-intercept is at -5, or namely when the line hits the y-axis is at -5, that's when x = 0, so the point is really (0 , -5), and we also know another point on the line, that is (-1 ,6), to get the equation of any straight line, we simply need two points off of it, so let's use those two

`\stackrel{y-intercept}{(\stackrel{x_1}{0}~,~\stackrel{y_1}{-5})}\qquad (\stackrel{x_2}{-1}~,~\stackrel{y_2}{6}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{6}-\stackrel{y1}{(-5)}}}{\underset{run} {\underset{x_2}{-1}-\underset{x_1}{0}}} \implies \cfrac{6 +5}{-1} \implies \cfrac{ 11 }{ -1 } \implies - 11`

`\begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-5)}=\stackrel{m}{- 11}(x-\stackrel{x_1}{0}) \implies y +5 = - 11 ( x -0) \\\\\\ y+5=-11x\implies {\Large \begin{array}{llll} y=-11x-5 \end{array}}`