Question

Use the four functions shown.

1. f (x) = e Superscript (4 minus x). 2. f (X) StartAbsoluteValue 4 minus x EndAbsoluteValue. 3. f (x) = RootIndex 3 StartRoot 4 minus x EndRoot. 4. f (x) = (4 minus x) Superscript two-thirds.

Which function is differentiable for all values of x over the interval (–5, 5)?

I
II
III
IV

Answer 1

Function I

Explanation:

Differentiate each function.

Function I

`f(x)=e^(4-x)`

`\boxed{\begin{minipage}{5.5 cm}\underline{Differentiating $e^(f(x))$}\\\\If $y=e^(f(x))$, then $\frac{\text{d}y}{\text{d}x}=f\:'(x)e^(f(x))$\\\end{minipage}}`

`f'(x)=-e^(4-x)`

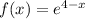
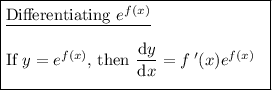
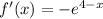
The domain of f'(x) is all real numbers: (-∞, ∞)

Therefore f(x) is differentiable for all values of x over the interval (-5, 5).

Function II

`f(x)=|4-x|`

`\boxed{\begin{minipage}{6.5 cm}\underline{Differentiating an absolute value function}\\\\$|f(x)|'=(f(x))/(|f(x)|)f'(x)$\\\end{minipage}}`

`f'(x)=-(4-x)/(|4-x|)`

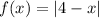
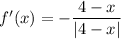
The domain of f'(x) is all real numbers except x = 4: (-∞, 4) ∪ (4, ∞)

Therefore, f(x) is not differentiable for all values of x over the interval (-5, 5).

Function III

`\begin{aligned}f(x)&=\sqrt[3]{4-x}\\&=(4-x)^{(1)/(3)}\end{aligned}`

`\boxed{\begin{minipage}{7 cm}\underline{Differentiating $[f(x)]^n$}\\\\If $y=[f(x)]^n$, then $\frac{\text{d}y}{\text{d}x}=n[f(x)]^(n-1) f'(x)$\\\end{minipage}}`

Therefore:

`\begin{aligned}f'(x)&=(1)/(3)(4-x)^{(1)/(3)-1} \cdot -1\\&=-(1)/(3)(4-x)^{-(2)/(3)}\\&=-\frac{1}{3(4-x)^{(2)/(3)}}\end{aligned}`

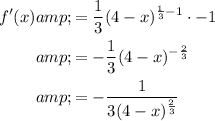
The domain of f'(x) is all real numbers except x = 4: (-∞, 4) ∪ (4, ∞)

Therefore, f(x) is not differentiable for all values of x over the interval (-5, 5).

Function 4

`f(x)=(4-x)^{(2)/(3)}`

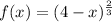
`\boxed{\begin{minipage}{7 cm}\underline{Differentiating $[f(x)]^n$}\\\\If $y=[f(x)]^n$, then $\frac{\text{d}y}{\text{d}x}=n[f(x)]^(n-1) f'(x)$\\\end{minipage}}`

Therefore:

`\begin{aligned}f'(x)&=(2)/(3)(4-x)^{(2)/(3)-1} \cdot -1\\&=-(2)/(3)(4-x)^{-(1)/(3)}\\&=-\frac{2}{3(4-x)^{(1)/(3)}}\end{aligned}`

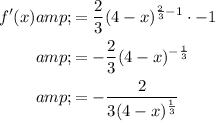
The domain of f'(x) is all real numbers except x = 4: (-∞, 4) ∪ (4, ∞)

Therefore, f(x) is not differentiable for all values of x over the interval (-5, 5).