Question

On a coordinate grid, line j passes through points (8, 2) and (-2,-2). On the same grid, line k

passes through points (-4, 3) and (-6, 8). Are lines j and k parallel, perpendicular, or neither?

Answer 1

Answer: lines j and k are perpendicular

Explanation:

Let's find the equations of lines j and k

`\displaystyle\\\boxed{(x-x_1)/(x_2-x_1)=(y-y_1)/(y_2-y_1) }`

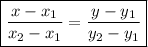
Line j: (8,2) (-2,-2)

x₁= 8 x₂=-2 y₁=2 y₂=-2

`\displaystyle\\(x-8)/(-2-8)=(y-2)/(-2-2) \\\\(x-8)/(-10)=(y-2)/(-4) \\\\`

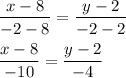
Multiply both parts of the equation by -4:

`\displaystyle\\(2)/(5) (x-8)=y-2\\\\(2)/(5) x-(16)/(5) =y-2\\\\(2)/(5) x-3.2+2=y-2+2\\\\(2)/(5)x-1.2=y\\\\ Thus,\ y=(2)/(5)x-1.2`

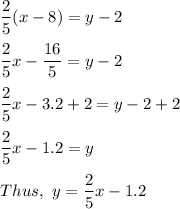
Line k: (-4,3) (-6,8)

x₁=-4 x₂=-6 y₁=3 y₂=8

`\displaystyle\\(x-(-4))/(-6-(-4)) =(y-3)/(8-3) \\\\(x+4)/(-6+4)=(y-3)/(5) \\\\(x+4)/(-2) =(y-3)/(5)`

Multiply both parts of the equation by 5:

`\displaystyle\\-(5)/(2)(x+4)=y-3\\\\ -(5)/(2)x-10=y-3\\\\ -(5)/(2)x-10+3=y-3+3\\ -(5)/(2)x-7=y\\Thus,\ y=-(5)/(2) x-7`

Hence, lines j and k are perpendicular