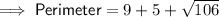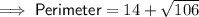Answer:
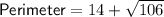
Explanation:
The perimeter of a two-dimensional shape is the distance all the way around the outside.
Given vertices:
As vertices (1, 5) and (1, -4) have the same x-coordinate, the measure of the line segment connecting the two points is the difference between their y-coordinates:
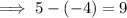
As vertices (1, -4) and (-4, -4) have the same y-coordinate, the measure of the line segment connecting the two points is the difference between their x-coordinates:
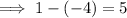
Finally, to find the measure of the line segment connecting points (1, 5) and (-4, -4), use the distance formula:
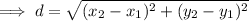
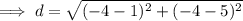
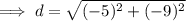
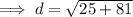
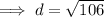
Therefore, the perimeter of the given triangle is the sum of the found side lengths: