Question

Please answer this question with steps. I will give 20 points if the answer is correct. Thank you.

Answer 1

y = 3x -√2

Explanation:

You want the tangent to the curve defined by x²(x² +y²) = y² at the point (√2/2, √2/2).

Slope

The slope of the tangent line is the derivative of the function at that point. The given equation can be rearranged to ...

y² = x⁴/(1 -x²)

Then the derivative is ...

2yy' = ((1 -x²)(4x³) -(x⁴)(-2x))/(1 -x²)²

Dividing by 2y gives ...

`y'=\frac{(2x^3(1-x^2)+x^5)/((1-x^2)^2)}{\sqrt{(x^4)/((1-x^2))}}=(x^3(2-2x^2+x^2)√(1-x^2))/(x^2(1-x^2)^2)=\frac{x(2-x^2)}{(1-x^2)^{(3)/(2)}}`

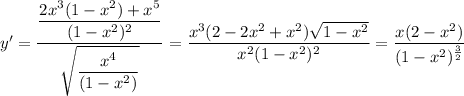
Evaluating this expression at x=√2/2, we find the slope to be ...

`y'=\frac{2^{-(1)/(2)}(2-2^(-1))}{(1-2^(-1))^{(3)/(2)}}=\frac{(3)/(2)}{(2^{(1)/(2)})(2^{-(3)/(2)})}=3`

Point-slope equation

The point-slope equation of the tangent line is ...

y -k = m(x -h) . . . . . . . . line with slope m through point (h, k)

y -√2/2 = 3(x -√2/2) . . . . line with slope 3 through point (√2/2, √2/2)

Rearranging to slope-intercept form, we get ...

y = 3x -3√2/2 +√2/2 . . . . . eliminate parentheses, add √2/2

y = 3x -√2 . . . . . . . . . . . . collect terms

__

Additional comment

We noticed that the given point (√3/2, √3/2) does not satisfy the equation, so we went looking for a point on the line y=x that does satisfy the equation. We found that (√2/2, √2/2) is on the graph, so we suspect a typo in the original problem statement. This answer gives the equation of the tangent line through the point (√2/2, √2/2).