Question

‼️SOMEONE HELP‼️

Simply. Express your answer using positive exponents
(r ^ - 8 * s ^ - 1 * t ^ - 1 * u ^ 7)/(r ^ 6 * s ^ 0 * t ^ - 9 * u * r ^ - 1 * s ^ - 7 * t ^ 0 * u ^ 0)​

Answer 1

`\huge \tt\dag \: Answer :`

`\tt \frac{ {r}^( - 8) {s}^( - 1) {t}^( - 1) {u}^(7) }{ {r}^(6) {s}^(0) {t}^( - 9) u \: • \: {r}^( - 1) {s}^( - 7) {t}^(0) {u}^(0) }`

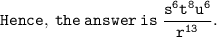
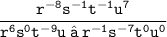
Now, put every term with power 0 = 1 i.e,

• s⁰ = 1
• t⁰ = 1
• u⁰ = 1

`\tt : \implies\frac{ {r}^( - 8) {s}^( - 1) {t}^( - 1) {u}^(7) }{ {r}^(6) * 1 * {t}^( - 9) u \: • \: {r}^( - 1) {s}^( - 7) * 1 * 1 } \\ \tt : \implies\frac{ {r}^( - 8) {s}^( - 1) {t}^( - 1) {u}^(7) }{ {r}^(6) {t}^( - 9) u \: • \: {r}^( - 1) {s}^( - 7) }`

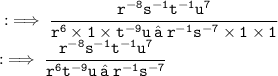
Now, move all terms with negative powers from numerator to denominator and denominator to numerator to make their powers positive.

`\tt : \implies\frac{ {r}^( 1) {s}^( 7) {t}^( 9) {u}^(7) }{ {r}^(6) {t}^( 1) u \: • \: {r}^( 8) {s}^( 1) }`

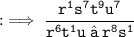
Now, cancel the terms that are getting cancelled.

`\tt : \implies\frac{ \cancel{{r}^( 1)}{s}^{ \cancel{7}} {t}^{ \cancel{9}} {u}^{ \cancel{7}} }{ {r}^{ \cancel{6}} \cancel{{t}^( 1)} \cancel{u} \: • \: {r}^( 8) \cancel{{s}^( 1)} } \\ \tt : \implies\frac{ {s}^( 6) {t}^( 8) {u}^(6) }{ {r}^(5) \: • \: {r}^( 8)}`

Now, add the powers of of exponential expression having same base.

`\tt : \implies\frac{ {s}^( 6) {t}^( 8) {u}^(6) }{ {r}^((5 + 8))} \\ \tt : \implies\frac{ {s}^( 6) {t}^( 8) {u}^(6) }{ {r}^(13)}`

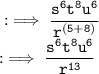
Hence, the answer is \dfrac{ {s}^{ 6} {t}^{ 8} {u}^{6} }{ {r}^{13}}.

`\large \tt Hence, \: the \: answer \: is \: \frac{ {s}^( 6) {t}^( 8) {u}^(6) }{ {r}^(13)}.`