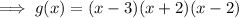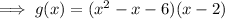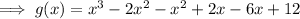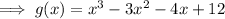Using a given zero to write a polynomial as a product of linear factors: real zeros For the polynomial below, 3 is a zero. g(x)=x³ - 3x² - 4x + 12 Express g(x) as a product of l…

Question

asked Oct 11, 2023 142k views

1 Answer

GFu · Answer 1 · 2023-10-18T20:52:42+0000

Answer:

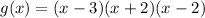
g(x)=(x-3)(x+2)(x-2)

Explanation:

Given:

Factor Theorem

If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x).

Therefore, if 3 is a zero of g(x), then g(3) = 0 and so (x - 3) is a factor of g(x):

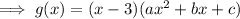
$\implies g(x)=(x-3)(ax^2+bx+c)$

As the leading coefficient of g(x) is one, a = 1:

$\implies g(x)=(x-3)(x^2+bx+c)$

As the constant of g(x) is 12, c = 12 ÷ -3 = -4:

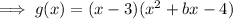
$\implies g(x)=(x-3)(x^2+bx-4)$

Expand:

$\implies g(x)=x^3+bx^2-4x-3x^2-3bx+12$

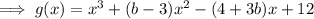
$\implies g(x)=x^3+(b-3)x^2-(4+3b)x+12$

Compare the coefficients of the terms in x² to find b:

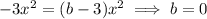
$-3x^2=(b-3)x^2 \implies b=0$

Therefore:

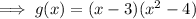
$\implies g(x)=(x-3)(x^2-4)$

$\boxed{\begin{minipage}{5 cm}\underline{Difference of Two Squares}\\\\$a^2-b^2=(a+b)(a-b)\\ \end{minipage}}$

To factor (x² - 4), rewrite as (x² - 2²) and apply the difference of two squares:

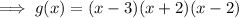
$\implies g(x)=(x-3)(x+2)(x-2)$

Therefore, the function g(x) as a product of linear factors is:

Check by expanding the factored function:

$\implies g(x)=(x-3)(x+2)(x-2)$

$\implies g(x)=(x^2-x-6)(x-2)$

$\implies g(x)=x^3-2x^2-x^2+2x-6x+12$

$\implies g(x)=x^3-3x^2-4x+12$