Question

Based on this projection, which of the following is closest to the number of t-shirts Marcus needs to sell during the first month to meet his goal? (100 brainley points plsss help)

Answer 1

A. 1,500

Explanation:

`\boxed{\begin{minipage}{7cm}\underline{Sum of the first n terms of a geometric series}\\\\$S_n=(a(1-r^n))/(1-r)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\ \phantom{ww}$\bullet$ $r$ is the common ratio.\\ \phantom{ww}$\bullet$ $n$ is the $n$th term.\\\end{minipage}}`

The given scenario can be modelled as a geometric series.

If Marcus' goal is to sell 15,000 t-shirts during the first 6 months, then:

• Sum Sₙ = 15,000
• n = 6

If he projects that the number of t-shirts he sells will increase by 20% each month then the common ratio is:

• r = (1 + 0.2) = 1.2

Substitute these values into the formula and solve for a:

`\implies 15000=(a(1-1.2^6))/(1-1.2)`

`\implies 15000(1-1.2)=a(1-1.2^6)`

`\implies a=(15000(1-1.2))/(1-1.2^6)`

`\implies a=1510.586188`

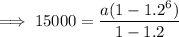
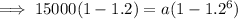
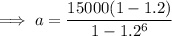
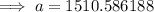
Therefore, the approximate number of T-shirts Marcus needs to sell during the first month to meet his goal is 1,500.

Check:

• Month 1 = 1511
• Month 2 = 1511 × 1.2 = 1813
• Month 3 = 1813 × 1.2 = 2176
• Month 4 = 2176 × 1.2 = 2611
• Month 5 = 2611 × 1.2 = 3133
• Month 6 = 3133 × 1.2 = 3760

Total = 1511 + 1813 + 2176 + 2611 + 3133 + 3760 = 15004

Check:

• Month 1 = 1500
• Month 2 = 1500 × 1.2 = 1800
• Month 3 = 1800 × 1.2 = 2160
• Month 4 = 2160 × 1.2 = 2592
• Month 5 = 2592 × 1.2 = 3110
• Month 6 = 3110 × 1.2 = 3732

Total = 1500 + 1800 + 2160 + 2592 + 3110 + 3732 = 14894 ≈ 15000