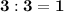1 Answer

Kanwal · Answer 1 · 2023-05-13T09:08:08+0000

The greatest common factor of 15, 12, and 24 is 3, since

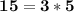
$\bold{15 = 3 * 5}$

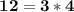
$\bold{12 = 3 * 4}$

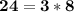
$\bold{24 = 3 * 8}$

Therefore, there is no number greater than 3 that is a common divisor of 15, 12 and 24.

If we divide 15, 12 and 24 by 3 we get:

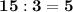
$\bold{15 : 3 = 5}$

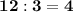
$\bold{12 : 3 = 4}$

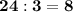
$\bold{24 : 3 = 8}$

The greatest common factor of 5,4, and 8 is I, since there is no number greater than I that is a factor of 15, 12, and 24.

So, let's observe that the result is
$\bold{3 : 3 = 1}$

Please log in or register to add a comment.