Answer:
Approximately
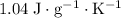 .
.
Step-by-step explanation:
Multiply energy input by efficiency to find the useful energy output:
 .
.
In other words,
 of energy was supplied to the air in the building.
of energy was supplied to the air in the building.
The standard unit of energy is Joules (
 .) Apply unit conversion:
.) Apply unit conversion:
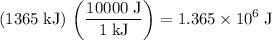 .
.
Let
 denote the specific heat capacity of the air in this building. Let
denote the specific heat capacity of the air in this building. Let
 denote the mass of the air.
denote the mass of the air.
Let
 denote the energy supplied to the air. Let
denote the energy supplied to the air. Let
 denote the change in temperature. The equation
denote the change in temperature. The equation
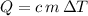 relates these quantities.
relates these quantities.
In this question, the change in the temperature of the air in this building is:
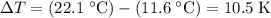 .
.
Rearrange the equation
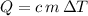 to find specific heat capacity
to find specific heat capacity
 :
:
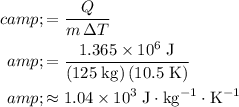 .
.