Question

Find zeros of quadratic polynomial
x²+x -20
​

Answer 1

Answer:m,m,

Explanation:

Answer 2

Zeros:

• x = -5
• x = 4

Explanation:

Given quadratic polynomial:

`x^2+x -20`

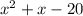
The zeros of a function f(x) are the x-values that satisfy the equation f(x)=0.

Therefore, to find the zeros of the given function, set it to zero and solve for x.

Factor the quadratic:

`\implies x^2+x-20=0`

`\implies x^2+5x-4x-20=0`

`\implies x(x+5)-4(x+5)=0`

`\implies (x-4)(x+5)=0`

`\boxed{\begin{minipage}{8.4 cm}\underline{Zero Product Property}\\\\If $a \cdot b = 0$ then either $a = 0$ or $b = 0$ (or both).\\\end{minipage}}`

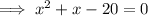
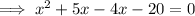
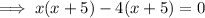
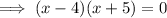
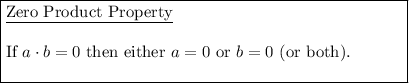
Apply the Zero Product Property:

`\implies x-4=0 \implies x=4`

`\implies x+5=0 \implies x=-5`

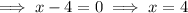
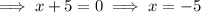
Therefore, the zeros of the given quadratic polynomial are:

• x = -5
• x = 4