Question

A die is rolled. Find the probability of the given event.

Write your answers as whole numbers or simplified fractions.
A. The number showing is a 2
P(2)=
B. The number showing is an even number
P(even) =
C. The number showing is greater than 5
P(greater than 5) =


No bots pls

Answer 1

`\textsf{A)} \quad \sf P(2)=(1)/(6)`

`\textsf{B)} \quad \sf P(even)=(1)/(2)`

`\textsf{C)} \quad \sf P(greater\;than\;5)=(1)/(6)`

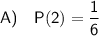
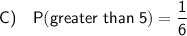
Explanation:

Probability is a measure of the likelihood or chance that an event will occur, expressed as a number between 0 (indicating impossibility) and 1 (indicating certainty).

The probability of an event occurring can be calculated by dividing the number of ways it can occur by the total number of possible outcomes:

`\boxed{\sf Probability\:of\:an\:event\:occurring = (Number\:of\:ways\:it\:can\:occur)/(Total\:number\:of\:possible\:outcomes)}`

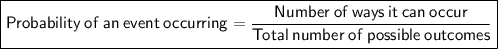
A standard die is a six-sided cube with numbered faces from 1 to 6. Therefore, the total number of possible outcomes when a die is rolled is 6.

Part A

Since there is only one face on the die numbered as 2, the probability of rolling a 2 is:

`\sf P(2)=(1)/(6)`

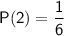
Part B

Since there are three even-numbered faces on the die (2, 4, and 6), the probability of rolling an even number is:

`\sf P(even)=(3)/(6)=(3 / 3)/(6 / 3)=(1)/(2)`

Part C

Since there is one face on the die with a number greater than 5, the probability of rolling a number greater than 5 is:

`\sf P(greater\;than\;5)=(1)/(6)`