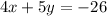Answer:
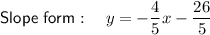

Explanation:

Given equation:

Rewrite in slope-intercept form:
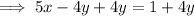
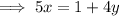
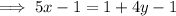
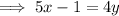
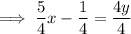
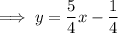
Therefore, the slope of the line is ⁵/₄.
If two lines are perpendicular to each other, their slopes are negative reciprocals.
Therefore, the slope of the perpendicular line is -⁴/₅.
Substitute the found slope -⁴/₅ and given point (1, -6) into the slope-intercept formula and solve for b:
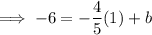
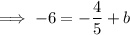
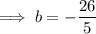
Therefore, the equation of the perpendicular line in slope form is:
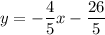
Multiply both sides of the equation in slope form by 5:
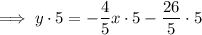
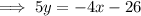
Add 4x to both sides:
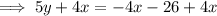
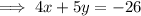
Therefore, the equation of the perpendicular line in standard form is: