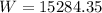Question

how much work is it to push a box (mass 200 kg) up an incline (angle 20 degrees with the horizontal) that is 8.6 meters long, if the coefficient of kinetic friction between the box and the incline is 0.6?

Answer 1

15284.35 Joules

Step-by-step explanation:

Here is an equation we can use.

Work + Initial PE + Initial KE = Final PE + Final KE + heat lost

`W+mgh_i+(1)/(2)mv_i^(2) =mgh_f+(1)/(2)mv_f^(2)+F_Fd`

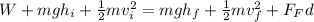
Solving for W gives us.

`W=-(mgh_i)-((1)/(2)mv_i^(2)) +mgh_f+(1)/(2)mv_f^(2)+F_Fd`

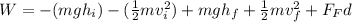
In this case we can assume the initial height is 0. So there is no Initial PE.

We can assume the box started at 0 m/s. So there is no Initial KE

The box gained height as it moved up the incline. So there is Final PE.

We can assume the box moved at a constant speed. There was no acceleration on the box. So there is no Final KE.

`F_F=F_N*u_k`

`F_N=mgcos(B)`

`F_F=mgcos(B)*u_k`

`W=mgh_f+F_Fd`

`W=mgh_f+mgcos(B)*u_k*d`

`h_f=d*sin(B)`

`W=m*g*d*sin(B)+m*g*cos(B)*u_k*d`

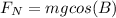
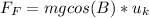
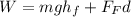
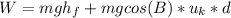
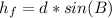
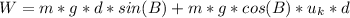
Lets solve for
`W`

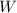
We are given

`m=200`

`g=9.81`

`B=20`

`u_k=0.6`

`d=8.6`

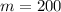
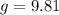
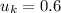
Replace the variables with our given numbers.

`W=200*9.81*8.6*sin(20)+200*9.81*cos(20)*0.6*8.6`

`W=15284.35`