Question

This is the Hamming space for k=3. Start at a vertex. Change one bit to cross one edge. Change two bits to cross two edges. Change three bits to cross three edges. Note the important difference between Hamming space and the everyday notion of numeric distance. Whereas we would normally say that 100 (4 in binary) and 000 (0 in binary) are 4 units apart, in Hamming space, they are only one unit apart, and very close.

We can start with some easy cases. For instance, if n = 2^k, then D = 1. Also, if n = 2, then D = k. This is clearly illustrated by the picture above. Note that the points furthest apart in Hamming space are on opposite corners of the cube, and that those corners have exactly inverse polarities.

Answer 1

The resultant equation will be,

D =
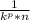`(1)/(k^(p) * n)` + c

According to the given question,

Hamming space is given, k = 3

Binary components are given in decimals,

4 = 100

0 = 000

Let us consider the linear solution for any equation,

y = mx + b

y = D

x = n

m = f(n)

b= y-intercept, What is D if k = 0

Calculating the value for m,

if D = maximum then n = 1

if D = minimum then n =
`2^{(k)/(2) }`

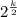
m =
`(y1-y2)/(x1-x2)`

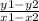
m =
`(k-1)/(1-2^(k-1) /2)`

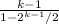
after solving,

m =
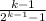`(k-1)/(2^(k-1) -1)` ------ equation 1

For calculating the value for b we do not know what n = 0 means so let us consider a known point on the line ( n = 1, D = k )

D = mx + b

k = mn + b

k - m = b

b = k + [
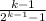`(k-1)/(2^(k-1) -1)` ] ------- equation 2

Putting together both equations,

D = -[
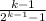`(k-1)/(2^(k-1) -1)`] n + k + [
`(k-1)/(2^(k-1) -1)` ]

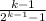∴ At every level, you have more elements you could add while keeping the hamming distance the same as you had at the previous level.

Therefore, the resultant equation will be,

D =
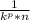`(1)/(k^(p) * n)` + c