Question

A 50 kg girl is standing in a lift which is accelerating upwards at 3 m/s^2. What will be the upward force from the lift floor on the girl's feet (in N)?

Answer 1

Approximately
`641\; {\rm N}` (assuming that
`g = (-9.81)\; {\rm N \cdot kg^(-1)}`.)

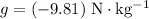Step-by-step explanation:

Forces on this person:

• Weight (downward, from the earth).
• Normal force (the upward force from the floor of the elevator.)

Let
`m` denote the mass of this person. It is given that
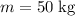`m = 50\; {\rm kg}`. The weight of this person will be:

`\begin{aligned}(\text{weight}) &= m\, g \\ &= (50\; {\rm kg})\, ((-9.81)\; {\rm N\cdot kg^(-1)}) \\ &\approx 490.5\; {\rm N}\end{aligned}`.

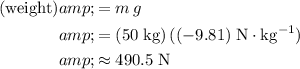(The value of weight is negative since weight points downwards.)

Let
`a` denote the acceleration of this person. It is given that
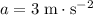`a = 3\; {\rm m\cdot s^(-2)}` (since this person is accelerating upwards, the value of
`a` will be positive.) The net force on this person will be:

`\begin{aligned}(\text{net force}) &= (\text{mass})\, (\text{acceleration})\\ &= (50\; {\rm kg})\, (3\; {\rm m\cdot s^(-2)}) \\ &\approx 150\; {\rm N}\end{aligned}`.

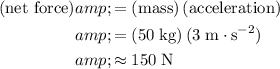Note that this net force is also equal to the vector sum of all the forces on this person. In other words:

`\begin{aligned}(\text{net force}) &= (\text{weight}) + (\text{normal force})\end{aligned}`.

Rearrange this equation to find
`(\text{normal force})`:

`\begin{aligned}(\text{normal force}) &= (\text{net force}) - (\text{weight}) \\ &\approx 150\; {\rm N} - ((-490.5)\; {\rm N}) \\ &\approx 641\; {\rm N}\end{aligned}`.

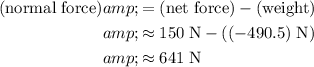Hence, the upward force on this person from the floor of the elevator will be approximately
`641\; {\rm N}`.