Observed that 7 is a divisor of 14, 21 and 28.
So in effect:
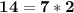

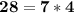
Thus, adding member by member the previous equalities, we would have:

Taking out the common factor of 7 in the previous expression, we will have:

I mean:
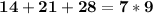
That is to say, that 7 is a divisor of the sum
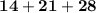 since it is contained exactly 9 times in said sum.
since it is contained exactly 9 times in said sum.