Question

The equation of a line in point-slope form is given below:

y + 4 = 2(x + 1)

What is the equation of this line written in Standard Form?


A. -2x + y = -2


B. 2x - y = -2


C. -2x - y = -2


D. 2x + y = 2

Answer 1

We must translate the equation from y-y1=m(x-x1) to ax+by=c from.

Distribute the 2 into x and 1

y+4=2x+2

Combine like terms and move terms:

-2x+y=-4+2

Simplify:

-2x+y=-2

-2x+y=-2 is in standard form

Answer 2

`\textsf{A.} \quad -2x + y = -2`

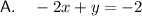
Explanation:

`\boxed{\begin{minipage}{5.5 cm}\underline{Standard form of a linear equation}\\\\$Ax+By=C$\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are constants. \\ \phantom{ww}$\bullet$ $A$ must be positive.\\\end{minipage}}`

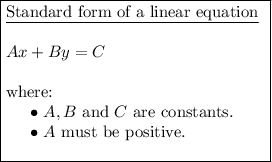
Given equation:

`y + 4 = 2(x + 1)`

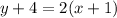
Distribute the right side of the equation:

`\implies y+4=2x+2`

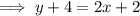
Subtract 2 from both sides:

`\implies y+4-2=2x+2-2`

`\implies y+2=2x`

Subtract y from both sides:

`\implies y+2-y=2x-y`

`\implies 2=2x-y`

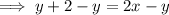
Switch sides:

`\implies 2x-y=2`

Therefore, the equation of the line written in standard form is:

`\boxed{2x-y=2}`

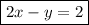
Since this is not one of the answer options, switch the signs:

`\implies -2x+y=-2`

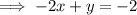
Please note that this is not in standard form, since the coefficient of the term in x is negative. However, as the equation in strict standard form is not a given answer option, the only answer can be -2 + y = -2.