Question

How much should you deposit at the end of each month in an IRA that pays 11% compounded monthly to earn ​$50000 per year from interest​ alone, while leaving the principal​ untouched, to be withdrawn at the end of each year after you retire in 30 years?

Answer 1

$154.07

Explanation:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

First find the Future Account Value (target amount) you need at the beginning of your retirement in order to earn $50,000 of interest each year whilst leaving the principal untouched.

Given:

• A = P + $50,000
• P = P
• r = 11% = 0.11
• n = 12 (monthly)
• t = 1 year

Substitute the values in the compound interest formula to find the Future Account Value:

`\implies P+50000=P\left(1+(0.11)/(12)\right)^(12 \cdot 1)`

`\implies P+50000=P\left((1211)/(1200)\right)^(12)`

`\implies 50000=P\left((1211)/(1200)\right)^(12)-P`

`\implies 50000=P\left(\left((1211)/(1200)\right)^(12)-1\right)`

`\implies P=(50000)/(\left(\left((1211)/(1200)\right)^(12)-1\right))`

`\implies P=432081.77`

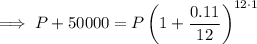
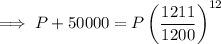
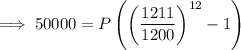
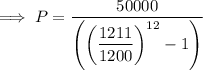
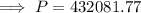
Therefore, the Future Account Value needed at the beginning of your retirement is $432,081.77 to allow you to earn $50,000 per year from interest alone.

`\boxed{\begin{minipage}{8.5 cm}\underline{Savings Plan Formula}\\\\$ FV=PMT\left[(\left(1+(r)/(n)\right)^(nt)-1)/((r)/(n)) \right]$\\\\where:\\\\ \phantom{ww}$\bullet$ $FV =$ future value\\ \phantom{ww}$\bullet$ $PMT =$ periodic payment \\ \phantom{ww}$\bullet$ $r =$ APR (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ years \\ \phantom{ww}$\bullet$ $n =$ number of payments per year \\ \end{minipage}}`

Given:

• FV = $432,081.77
• r = 11% = 0.11
• t = 30 years
• n = 12 (monthly)

Substitute the values into the Savings Plan formula and solve for PMT to find the monthly payments:

`\implies 432081.77=PMT\left[(\left(1+(0.11)/(12)\right)^(12 \cdot 30)-1)/((0.11)/(12)) \right]`

`\implies 432081.77=PMT\left[(\left((1211)/(1200)\right)^(360)-1)/((11)/(1200)) \right]`

`\implies 432081.77=PMT\left[2804.519736 \right]`

`\implies PMT=(432081.77)/(2804.519736)`

`\implies PMT=154.0662255`

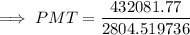
Therefore, you should deposit $154.07 at the end of each month to be able to withdraw $50,000 per year from interest alone at the end of each year after you retire in 30 years.