Answer:
$172,984.44 (nearest cent)
Explanation:

Given:
- P = $25,000
- r = 6.5% = 0.065
- n = 4 (quarterly)
- t = 30 years
Substitute the given values into the formula and solve for A:

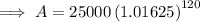
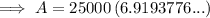
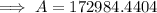
Therefore, if you deposit $25,000 now at 6.5% compounded quarterly, you will have $172,984.44 (nearest cent) in 30 years.