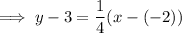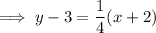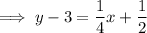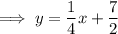Question

Which of the following is the equation of the line that is perpendicular to y = - 4x - 5 and goes through the point (-2, 3)?

O y = - 4x-5
Oy = 4x + 11
O y = x + 1/
O y = -x + 1/

Answer 1

`y=(1)/(4)x+(7)/(2)`

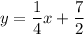
Explanation:

Given equation:

`y=-4x-5`

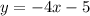
If two lines are perpendicular to each other, their slopes are negative reciprocals.

The slope of the given equation is -4.

Therefore, the slope of the perpendicular line is ¹/₄.

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

Substitute the found slope and point (-2, 3) into the point-slope formula to create the equation of the perpendicular line.

`\implies y-3=(1)/(4)(x-(-2))`

`\implies y-3=(1)/(4)(x+2)`

`\implies y-3=(1)/(4)x+(1)/(2)`

`\implies y=(1)/(4)x+(7)/(2)`