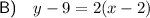Answer:
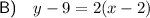
Explanation:
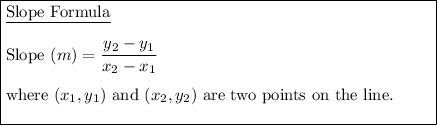
Given points:
Substitute the given points into the slope formula to find the slope of the line:
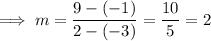

Substitute the found slope and point (-3, -1) into the point-slope formula:
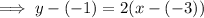
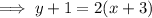
Substitute the found slope and point (2, 9) into the point-slope formula:
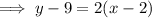
Therefore, the correct answer option is: