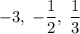Question

2: Using the fundamental theorem of algebra, factor the polynomial

completely. Then, list all the zeros of the polynomial.

f(x) = 6x³ + 19x² + 2x-3 given x = -3 is a solution.

Answer 1

`\textsf{Factored}: \quad f(x)=(x+3)(3x-1)(2x+1)`

`\textsf{Zeros}: \quad -3,\;-(1)/(2),\; (1)/(3)`

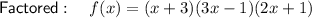
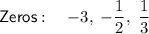
Explanation:

Fundamental Theorem of Algebra

Any polynomial of degree n has n roots.

Any polynomial has at least one solution.

Given polynomial:

`f(x)=6x^3+19x^2+2x-3`

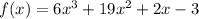
If x = -3 is a solution then (x + 3) is a factor of the polynomial:

`\implies f(x)=(x+3)(ax^2+bx+c)`

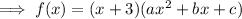
The leading coefficient of the given function is 6. Therefore, a = 6:

`\implies f(x)=(x+3)(6x^2+bx+c)`

The constant of the given function is -3. Therefore, x = -1:

`\implies f(x)=(x+3)(6x^2+bx-1)`

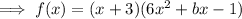
Expand:

`\implies f(x)=6x^3+bx^2-x+18x^2+3bx-3`

`\implies f(x)=6x^3+(b+18)x^2-(1-3b)x-3`

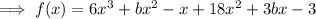
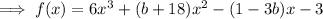
Compare the coefficients of the terms in x²:

`19=b+18 \implies b=1`

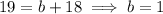
Therefore:

`\implies f(x)=(x+3)(6x^2+x-1)`

Factor (6x² + x - 1):

`\implies 6x^2+x-1`

`\implies 6x^2+3x-2x-1`

`\implies 3x(2x+1)-1(2x+1)`

`\implies (3x-1)(2x+1)`

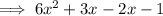
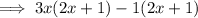
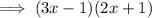
Therefore, the fully factored polynomial is:

`\implies f(x)=(x+3)(3x-1)(2x+1)`

To find the zeros, set f(x) = 0 and apply the zero-product property:

`\implies x+3=0 \implies x=-3`

`\implies 3x-1=0 \implies x=(1)/(3)`

`\implies 2x+1=0 \implies x=-(1)/(2)`

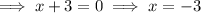
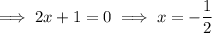
Therefore, the zeros of the polynomial are:

`-3,\;-(1)/(2),\; (1)/(3)`