Question

Un sector circular tiene un arco de 12 cm y un área de 245 cm², ¿Cuál es su radio?

Answer 1

Answer: r=40⁵/₆ cm

Explanation:

The area of the sector is equal to the product of the arc length of the sector by half the radius:

`\displaystyle\\A=L((1)/(2)r ) \ \ \ \ \ (1)`

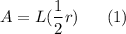
A - an area of the sector

L - the arc length of the sector

r - the radius of the sector

Multiply both parts of the equation (1) by 2:

`2A=Lr`

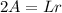
Divide both parts of the equation by L:

`\displaystyle\\(2A)/(L) =r\\\\Thus,\ r=(2A)/(L)`

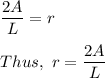
Hence,

`\displaystyle\\r=(2(245))/(12) \\\\r=(490)/(12) \\\\r=40(5)/(6)\ cm`

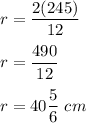
L: