Answer:
1.7 raised to the twenty eighth power over 1.6 raised to the twenty first power
Explanation:
Let's translate the wording to math form:
Worded question is:
1.6 cubed over 1.7 raised to the fourth power all raised to the power of negative seven
Break it down into parts to make it easier to understand
- 1.6 cubed ⇒ 1.6³
- 1.7 raised to the fourth power ⇒ 1.7⁴
- 1.6 cubed over 1.7 raised to the fourth power
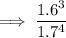
- 1.6 cubed over 1.7 raised to the fourth power all raised to the power of negative seven
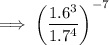
Simplify the above term. When a term with an exponent is raised to another exponent, then the resulting exponent is the product of the two exponents
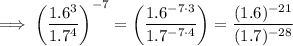
For negative exponents we have the rule
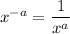
So, in this case since both numerator and denominator have negative terms , we simply switch them to get
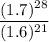
In words we can express this mathematical form as:
1.7 raised to the twenty eighth power over 1.6 raised to the twenty first power
Which is the answer.
Choices are not labeled and formatting is lost in your question so I cannot tell you which choice it is