Question

a pianist plans to play 3 pieces at a recital from her repertoire of 23 pieces, and is carefully considering which song to play first, second, etc. to create a good flow. how many different recital programs are possible?

Answer 1

10626 different recital programs possible

Explanation:

Since there is no repetition we can tackle this problem in the following manner.

Out of the 23 pieces, the pianist can choose the first one in 23 ways

Out of the remaining 22 pieces she can choose the second one in 22 different ways

Out of the remaining 21 pieces she can choose the third one in 21 different ways

So total number of ways in which 3 pieces can be played without repetition is 23 x 22 x 21 = 10,626 ways

There is a formula for this kind of situation
If there are a total of n items and you want to choose r items from this, the number of possible ways to do this without repetition is given by the formula

`_(n)P_(r) = (n!)/((n-r)!)`

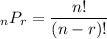
In this case, n = 23, r = 3 so we get

`_(23)P_(3) = (23!)/((23-3)!) = (23!)/(20!) = 23 * 22 * 21 = 10626`

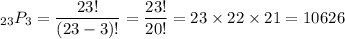
Same as the above