Question

A company sells widgets. The amount of profit, y, made by the company, is related to

the selling price of each widget, x, by the given equation. Using this equation, find out
the maximum amount of profit the company can make, to the nearest dollar,
y=
-x^2+78x-543

Answer 1

$978

Explanation:

Given:

• y = amount of profit
• x = selling price of each widget
• 
  `y=-x^2+78x-543`

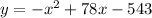
To find the maximum amount of profit, differentiate the equation, set it to zero and solve for x. Substitute found value of x into the original equation.

Differentiate equation

`y=-x^2+78x-543`

`\implies (dy)/(dx)=-2x+78`

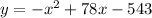
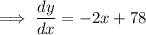
Set differentiated equation to zero and solve for x:

`(dy)/(dx)=0`

`\implies -2x+78=0`

`\implies 2x=78`

`\implies x=39`

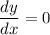
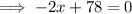
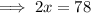
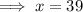
Maximum profit

Substitute x = 39 into the equation:

`\implies -(39)^2+78(39)-543=978`

Therefore, max profit is $978