Question

Which equation will yield the time it takes for the candles to burn down to the same height?

How much time will it take for the candles to burn down to the same height?

Answer 1

(i) Equation is

`12 - \displaystyle {(3)/(4)x = 18-3x\\\\`
This would be choice C

(ii) 2 hours and 40 minutes which is Choice A

Explanation:

Let the time taken for both candles to burn down to the same length be x hours

`\textrm{The rate at which the 12 inch candle burns } = (3)/(4) \textrm{ inches per hour}\\\\`

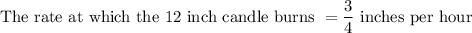
In time x hours, this candle would have burnt

`\displaystyle {(3)/(4)x \;}\textrm{inches}`

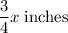
Height of 12" candle after x hours =

`12 - \displaystyle {(3)/(4)x \;}\textrm{inches}`

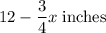
The 18" candle burns at the rate of 3" per hour
So height of candle after x hours = 18 - 3x

Both these quantities must be equal

`12 - \displaystyle {(3)/(4)x = 18-3x\\\\`

Solving for x:
1. Multiply both sides by 4
48 - 3x = 72 - 12x

2. Add 3x to both sides:
48 = 72 - 12x + 3x

48 = 72 - 9x

3. Subtract 72 from both sides:
48-72 = - 9x

==> -24 = -9x

4. Switch sides
-9x = -24

5. Multiply by -1
9x = 24

6. Divide by 9 to get

x = 24/9 = 2 2/3 hours

2/3 hour = 2/3 x 60 = 40 minutes

So total time taken for both candles to reach the same height is
2 hours and 40 minutes (Choice A)