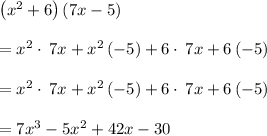Answer:
First choice:
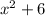
Explanation:
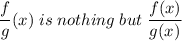
So you could divide
7x³-5 x²+42x-30 by 7x-5 and arrive at the correct answer.
But polynomial division is a pain
So instead we can multiply 7x -5 with each of the choices given and see which one will result in 7x³-5 x²+42x-30
But there is an easier way
- We can eliminate the second choice, 7x³+ 6 and last choice 7x³ 6. That is because there is a x³ term in the polynomial and its coefficient is 7
- Both of these incorrect choices will result in 7x² · 7x which is 49x³. So eliminate these two.
The first and third choices differ only in the sign of the constant
The second choice has +6 as the constant and the third has -6
Therefore the constant in the product should be either 6 · (-5) = -30 or
6(5) = 30
Since the coefficient of f(x) is -30, the correct answer is the first choice
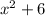
Verify: