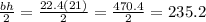Question

a) A larger triangle with a height of 21 cm is made in this way from smaller triangles with a height of 3 cm and an area of 4.8 cm", What is the area of this larger triangle?​

Answer 1

235.2

Explanation:

This is a multistep problem. We'll need to first find the base value of the smaller triangle using the area formula for a triangle:

`(bh)/(2)`

b <-- base

h<--- height

`(b3)/(2)=4.8`

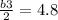
Solve for the b value

3b = 9.6 ---- multiply both sides by 2

b = 3.2 --- divide both sides by 3

3.2 is the base value of our smaller triangle.

Now, with this new information, we need to set up a proportion to find the base value of the larger triangle. A proportion is appropriate for this scenario because the larger triangle was a dilation from the smaller triangle.

`(21)/(b) =(3)/(3.2)`

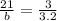
b --- represents the base value

Now solve the proportion by cross multiplying:

3b = 67.2

b = 22.4

Now we have the base value of our larger triangle. Finally, we can find the area of the larger triangle with the area formula:

`(bh)/(2) =(22.4(21))/(2) =(470.4)/(2) =235.2`