Question

A line passes through the point (6,-1) and is perpendicular to the line with the equation -2x + 3y = -6.

Answer 1

Answer: A

Explanation:

Before we find the equation of the perpendicular line, we have to find the slope of the original line.

The slope-intercept form of the equation is y=mx+b, so let's change that.

`-2x+3y=-6` [add both sides by 2x]

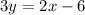`3y=2x-6` [divide both sides by 3]

`y=(2)/(3) x-2`

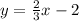
This gives slope as
`(2)/(3)`.

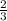There are 2 things for us to do to find the slope of a perpendicular line.

1. reciprocal

2. change sign

Let's apply those rules.

1.
`(3)/(2)`

2.
`-(3)/(2)`

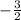
Now, we can find the perpendicular lines by plugging in our new point.

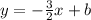`y=-(3)/(2) x+b` [plug in x and y]

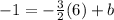`-1=-(3)/(2)(6)+b` [multiply]

`-1=-9+b` [add both sides by 9]

`b=8`

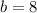
Now we can plug in for our slope-intercept equation.

`y=-(3)/(2) x+8`

Since answers are in standard form, we have to manipulate it.

`y=-(3)/(2) x+8` [add both sides by
`(3)/(2) x`]

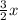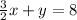`(3)/(2)x+y=8` [multiply both sides by 2]

`3x+2y=16`

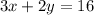
Therefore, our final answer is A.