Answer:
(-4, -1]
Explanation:
Given inequality:

When the denominator of a rational function is zero, the function is undefined. Therefore, x ≠ -4, so x = -4 is a boundary point for the solution to the inequality.
Solve the inequality as though it were an equation.
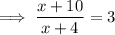
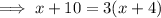
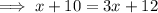

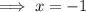
The real solution to the equation is also a boundary point for the solution to the inequality.
Make the x = -1 boundary point a closed circle as the original inequality includes equality.
Make the x = -4 boundary point an open circle as it is not included.
Three regions have been created:
Select points from the different regions and test to see if they satisfy the original inequality:
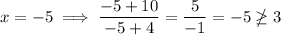
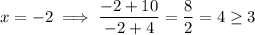
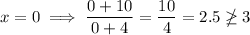
Since x = -5 does not satisfy the original inequality, the region x < -4 is not part of the solution.
Since x = -2 satisfies the original inequality, the region -4 > x ≤ -1 is part of the solution.
Since x = 0 does not satisfy the original inequality, the region x ≥ -1 is not part of the solution.
Therefore, the solution in interval notation is:
To graph the solution set:
- Place an open circle at x = -4.
- Place a closed circle at x = -1.
- Connect the circles with a line between them.