Question

NO LINKS!! Please help me with this problem. Part 6ff​

Answer 1

The sequence is not arithmetic. In an arithmetic sequence, the difference between consecutive terms is constant. However, in this sequence, the difference between the terms is not constant. For example, the difference between the first and second terms is 1^5 - 2^5 = -3, while the difference between the second and third terms is 2^5 - 3^5 = -6. Since the difference between consecutive terms is not constant, this sequence is not arithmetic. Therefore, the common difference is NONE.

Answer 2

No, the sequence is not arithmetic.

d = NONE

Explanation:

An Arithmetic Sequence has a common difference between each term (the difference between each term is the same).

Given sequence:

`1^5, 2^5, 3^5, 4^5, 5^5, ... = 1, 32, 243, 1024, 3125, ...`

Calculate the difference between each term:

`1 \underset{+31}{\longrightarrow} 32 \underset{+211}{\longrightarrow} 243 \underset{+781}{\longrightarrow} 1024 \underset{+2101}{\longrightarrow} 3125`

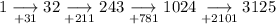
As the difference between each term is not constant, the sequence is not an arithmetic sequence.

Therefore, the common difference, d = NONE.