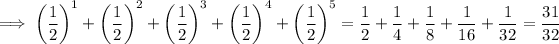Question

NO LINKS!! Please help me with this problem. Part 7ff​

Answer 1

`\textsf{a)} \quad (7)/(8)`

`\textsf{b)} \quad (15)/(16)`

`\textsf{c)} \quad (31)/(32)`

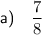
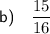
Explanation:

Given infinite series:

`\displaystyle \sum^(\infty)_(i=1) \left((1)/(2) \right)^(i)`

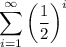
The sums of the first terms of the series are called partial sums.

(a) The third partial sum is the sum of the first three terms:

`\implies \left((1)/(2) \right)^(1)+\left((1)/(2) \right)^(2)+\left((1)/(2) \right)^(3)=(1)/(2)+(1)/(4)+(1)/(8)=(7)/(8)`

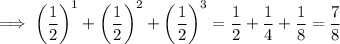
(b) The fourth partial sum is the sum of the first four terms:

`\implies \left((1)/(2) \right)^(1)+\left((1)/(2) \right)^(2)+\left((1)/(2) \right)^(3)+\left((1)/(2) \right)^(4)=(1)/(2)+(1)/(4)+(1)/(8)+(1)/(16)=(15)/(16)`

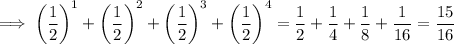
(c) The fifth partial sum is the sum of the first five terms:

`\implies \left((1)/(2) \right)^(1)+\left((1)/(2) \right)^(2)+\left((1)/(2) \right)^(3)+\left((1)/(2) \right)^(4)+\left((1)/(2) \right)^(5)=(1)/(2)+(1)/(4)+(1)/(8)+(1)/(16)+(1)/(32)=(31)/(32)`