Question

NO LINKS!! Please help me with this problem. Part 1ff​

Answer 1

`\textsf{a)} \quad A=(x(2x+22))/(x-4)`

`\textsf{b)} \quad x > 4`

`\begin{aligned}\text{c)} \quad x &= 11.75\; \sf in\\y &= 68.98\; \sf in \end{aligned}`

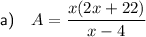
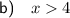
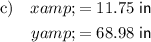
Explanation:

Part (a)

Print area (blue rectangle):

• width = (x - 4) in
• length = (y - 2) in
• area = 30 in²

Create an equation for the print area using the given values and rearrange to isolate y:

`\implies (x-4)(y-2)=30`

`\implies y-2=(30)/(x-4)`

`\implies y=(30)/(x-4)+2`

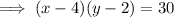
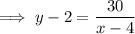
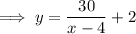
Total area of the page is:

`\implies A=xy`

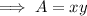
Substitute the found expression for y to write an equation for the total area of the page in terms of x:

`\implies A=x\left((30)/(x-4)+2\right)`

`\implies A=x\left((30+2(x-4))/(x-4)\right)`

`\implies A=x\left((2x+22)/(x-4)\right)`

`\implies A=(x(2x+22))/(x-4)`

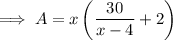
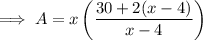
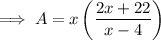
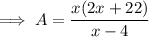
Part (b)

If x < 4 then A < 0.

If x = 4 then A is undefined.

Therefore, given the physical constraints of the problem, x has to be greater than 4.

Part (c)

Using a graphing utility, graph the function for area from part (a) when x > 4 (see attachment). (Note: The x-axis of the attached graph crosses the y-axis at y = 50 for ease of inspection).

The values of x and y that use the least amount of paper are the coordinates of the minimum point of the graph.

From inspection of the graph, the minimum point is:

• x = 11.75 in
• y = 68.98 in