Question

What are the zeros of
2x² = 3x+1?

Answer 1

`x = (√(17) + 3)/(4) , x = (√(17) - 3)/(4)`

Explanation:

Zeros of a quadratic function are the x-intercepts or solving it.

First, subtract 3x on both sides.

`2x^2-3x=3x-3x+1`

`2x^2-3x=1`

Divide both sides by 2, the value of a.

`(2x^2)/(2) - (3x)/(2) = (1)/(2)`

`x^2 - (3)/(2) x= (1)/(2)`

Add this to both sides, which makes it a perfect square:

`((a)/(2) )^2`

a is the coefficient of x.

`((3/2)/(2) )^2`

`((3)/(4) )^2`

`(9)/(16)`

`x^2 - (3)/(2) x + (9)/(16) = (1)/(2) + (9)/(16)`

`x^2-(3)/(2) x+(9)/(16) = (17)/(16)`

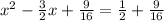
Factor out the left side.

`(x-(3)/(4) )^2 =(17)/(16) }`

Find the square root of both sides.

`\sqrt{(x-(3)/(4) )^2 }} = \sqrt{(17)/(16)}`

`x-(3)/(4) = (√(17) )/(4) , -\frac{√(17) }4}`

Add 3/4 on both sides.

`x = (√(17) + 3)/(4) , x = (√(17) - 3)/(4)`

Answer 2

The zeroes of given equation is 1 and 1/2

Explanation:

2x² = 3x + 1

2x² - 3x - 1 = 3x + 1 - 3x - 1

2x² - 3x - 1 = 0

Method used:

• Splitting the middle term

2x² - 2x - x - 1 = 0

2x(x - 1) - 1(x - 1) = 0

(x - 1) (2x - 1) = 0

x - 1 = 0 or 2x - 1 = 0

x = 1 or x = 1/2

Thus, The zeroes of given equation is 1 and 1/2