Question

(Offering Lots of Points) Please help me with this question!
​

Answer 1

`\Huge \boxed{ \texttt{\bf{y = x + 7.75} }}`

Explanation:

To find the linear function rule that models the cost
`\texttt{y}` of a package containing any number
`\texttt{x}` of comic books, we can use the given information:

• A poster and 4 comics cost $11.75

• A poster and 11 comics cost $18.75

Let's denote the cost of a poster as
`\texttt{P}` and the cost of a comic book as
`\texttt{C}`. Then, we can write two equations:

• 
  `\texttt{ P + 4C = 11.75}` (Equation 1)

• 
  `\texttt{P + 11C = 18.75}` (Equation 2)

To solve these equations, we can use the method of elimination. Let's use this method to eliminate
`$$P$$`:

• 
  `\texttt{(P + 11C) - (P + 4C) = 18.75 - 11.75}`

• 
  `\texttt{7C = 7}`

• 
  `\texttt{C = 1}`

Now, substituting the value of
`\texttt{C}` back into equation 1:

• 
  `\texttt{P + 4(1) = 11.75}`

• 
  `\texttt{P = 11.75 - 4}`

• 
  `\texttt{P = 7.75}`

Now that we have the cost of a poster (P) and a comic book (C), we can write the linear function rule as:

`\Large \boxed{\texttt{y = x + 7.75}}`

• 
  `\texttt{y}` is the total cost of a package

• 
  `\texttt{x}` is the number of comic books in the package.

Now, suppose another store sells a similar package modelled by a linear function rule with an initial value of $6.99. This means that the cost of a poster at the other store is $6.99. Since the cost of a comic book is the same at both stores ($1), the linear function rule for the other store is:

`\Large \boxed{ \texttt{y = x + 6.99}}`

Comparing the two linear function rules, we can see that the second store has a better deal because the initial cost of a poster is lower ($6.99) compared to the first store ($7.75).

________________________________________________________

Answer 2

Linear function: y = x + 7.75

Explanation:

A store sells packages of comic books with a poster. We are told that:

• A poster and 4 comics books cost $11 75.
• A poster and 11 comics books cost $18.75.

Let p be the cost of one poster.

Let c be the cost of one comic book.

Write a system of equations using the given information and the defined variables:

`\begin{cases}p + 4c = 11.75\\p + 11c = 18.75\end{cases}`

Subtract the first equation from the second equation to eliminate p:

`\begin{array}{crcrcl}&p&+&11c&=&18.75\\-&(p&+&4c&=&11.75)\\\cline{2-6}&&&7c&=&\;\;7.00\\\cline{2-6}\end{array}`

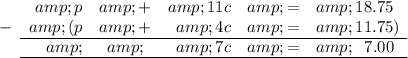
Solve for c:

`7c=7.00`

`c=1.00`

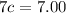
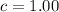
Therefore, the cost of one comic book is $1.00.

Substitute the found value of c into one of the equations and solve for p:

`\begin{aligned}p+4(1.00)&=11.75\\p+4.00&=11.75\\p&=7.75\end{aligned}`

Therefore, the cost of one poster is $7.75.

Now we know the cost of one poster and one comic, we can write a linear function that models the cost y of a package containing x number of comic books:

`y = 1.00x + 7.75`

`y =x + 7.75`

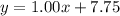
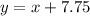
We are told that another store sells a similar package modeled by a linear function rule with initial value $6.99. The initial value is the y-intercept of each function, i.e. the cost of the package when zero comics are sold. So the linear function for this package is:

`y = x + 6.99`

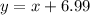
To determine which store has the better deal, we need to compare the y-intercepts (the initial values). The store with the lower initial value provides a better deal because it charges less for the basic package (when the number of comic books is zero).

Since 6.99 is less than 7.75, the other store offers a better deal, as it has a lower initial cost for the basic package.