Answer:
∠ABC=22°
∠BAC=68°
Explanation:
The sum of all angles in a triangle must equal 180°. If one of the angles is 90°, the sum of the other two angles must also be 90°. So, ∠ABC+∠BAC=90°. For this problem, let
∠ABC=2x+2°
∠BAC=6x+8°
So,
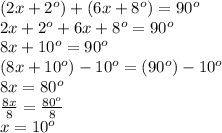
Replace x with 10° in the angle equations:
∠ABC=2(10°)+2°=22°
∠BAC=6(10°)+8°=68°
These angle measures can be confirmed by ensuring all angle measures total 180°:
22°+68°+90°=180°
180°=180°